Introduction to
PAGs + FCI + TFCI
EuroCIM 2024
April 16, 2024
No unmeasured confounders?
DAGs (and CPDAGs) assume no unmeasured/latent confounders (causal sufficiency). Often a strong assumption.
All 3 cases: \(X \centernot{\perp\mkern-9.5mu\perp}Y\).
Same conditional independencies (of observed variables)
Need something more to represent/visualize relationships
Latent/unmeasured confounders
If we can “imagine” latent confounders we can still use DAGs for causal inference and determine what we can estimate.
How to visualize the conditional independencies among the observed variables only for DAGs with observed and latent variables?
We could marginalize out all latent variables.
DAGs are not closed under marginalization so cannot be represented by a DAG
Maximal Ancestral Graphs (MAGs)
A maximal ancestral graph is a (directed) mixed ancestral graph that
- may contain two kinds of edges:
directed edges (→) and bi-directed edges (↔︎). - has no directed cycles
- an edge X ↔︎ Y means no directed path from X to Y, or Y to X.
- is maximal: no edge can be added without changing the independence model.
For DAGs we have \(d\)-separation. For MAGs we have \(m\)-separation.
Examples
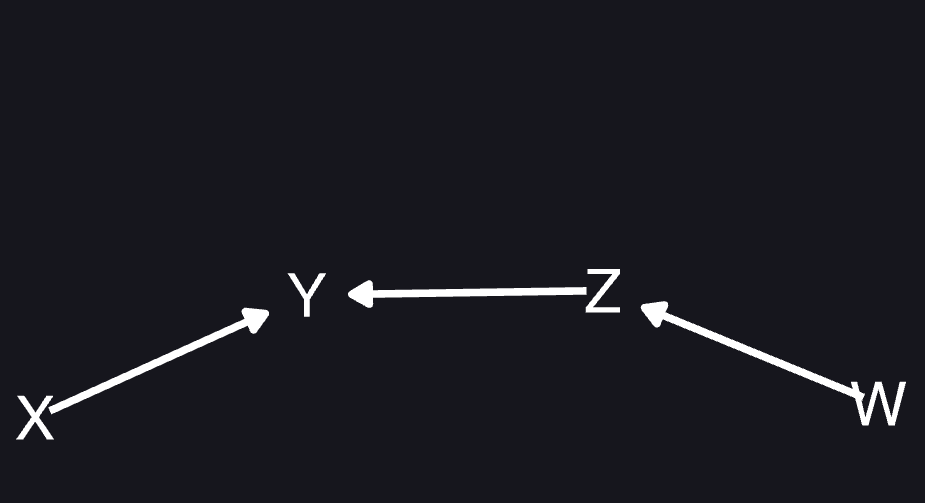
Partial Ancestral Graphs (PAGs)
Causal discovery can only hope to find a PAG = an equivalence classes of MAGs. Not the MAG.
Note: causal ancestors - not direct causes.
Three edgemarks in PAGs have the following interpretation:
- Blank: this blank is present in all MAGs in the equivalence class.
- Arrow: this arrow is present in all MAGs in the equivalence class.
- Circle: at least one MAG in the equivalence class has the edgemark as blank, and at least one has the edgemark as arrow.
Edge interpretation in PAGs
| Edge | Meaning |
|---|---|
| Directed \(X\rightarrow Y\) |
\(X\) is an ancestor of \(Y\), and there may further be unobserved confounding between the two |
| Bidirected \(X\longleftrightarrow Y\) |
unobs confounding between \(X\) and \(Y\), but no causal ancestral relationship in either direction |
| Possibly bidirected edge \(X \hbox{$\circ$}\kern-1.5pt\hbox{$\rightarrow$}Y\) |
either \(X \rightarrow Y\) or \(X\longleftrightarrow Y\) |
| Undetermined edge \(X \hbox{$\circ$}\kern-0.5pt\textemdash\kern-0.5pt\hbox{$\circ$}Y\) |
no info about the relationship between \(X\) and \(Y\). Either \(X \rightarrow Y\), \(X \leftarrow Y\) or \(X\leftrightarrow Y\). |
Examples

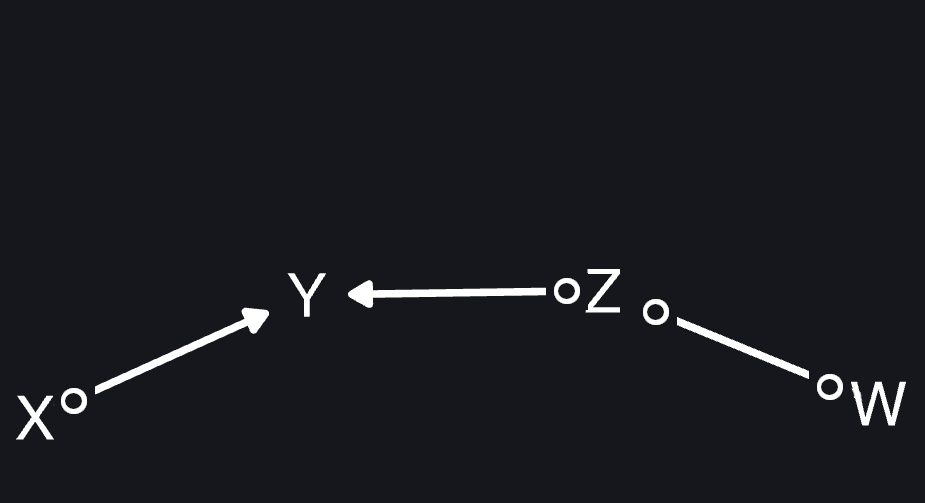
Fast Causal Inference (FCI)
- Start with fully connected graph
- Learn initial skeleton using tests of conditional independence
from neighbours. May contain too many edges due to sep-sets - Find \(v\)-structures (\(C \rightarrow A \leftarrow B\))
- Determine larger separation sets & test for conditional independence. Get new skeleton and \(v\)-structures.
- Orient remaining edges using ruleset
Result: a PAG
The temporal FCI algorithm (TFCI)
Extends the FCI algorithm to tiered information. Mimics TPC
- For conditional independence test between \(X\) and \(Y\) do not condition on the future: No variables from a later tier than both \(X\) and \(Y\) in the separating sets.
- Same modification here. No variables from a later tier than both \(X\) and \(Y\) in the separating sets.
- Orient remaining edges using ruleset. Start by setting arrowheads at latest node for edges spanning tiers.
References
P. Spirtes, C. Glymour, and R. Scheines. Causation, Prediction, and Search. The MIT Press, Cambridge, Massachusetts, 2nd ed., 2000.
P. Spirtes, C. Meek, and T. Richardson. An algorithm for causal inference in the presence of latent variables and selection bias. In Computation, Causation, and Discovery. 1999.
J. Zhang. On the completeness of orientation rules for causal discovery in the presence of latent confounders and selection bias. Artificial Intelligence, 172(16-17), 2008.
R Ali, T. Richardson, and P. Spirtes. Markov equivalence for ancestral graphs. The Annals of Statistics, 37(5B):2808–2837, 2009.