Lessons learned from predicting the 2018 FIFA World Cup results

# Lessons learned from predicting the 2018 FIFA World Cup results
### Claus Thorn Ekstrøm<br>UCPH Biostatistics<br>.small[<a href="mailto:ekstrom@sund.ku.dk">ekstrom@sund.ku.dk</a> ]
### November 12th, 2018<br>.small[Slides @ <a href="www.biostatistics.dk/talks/">biostatistics.dk/talks/</a>]

---

# Denmark vs Germany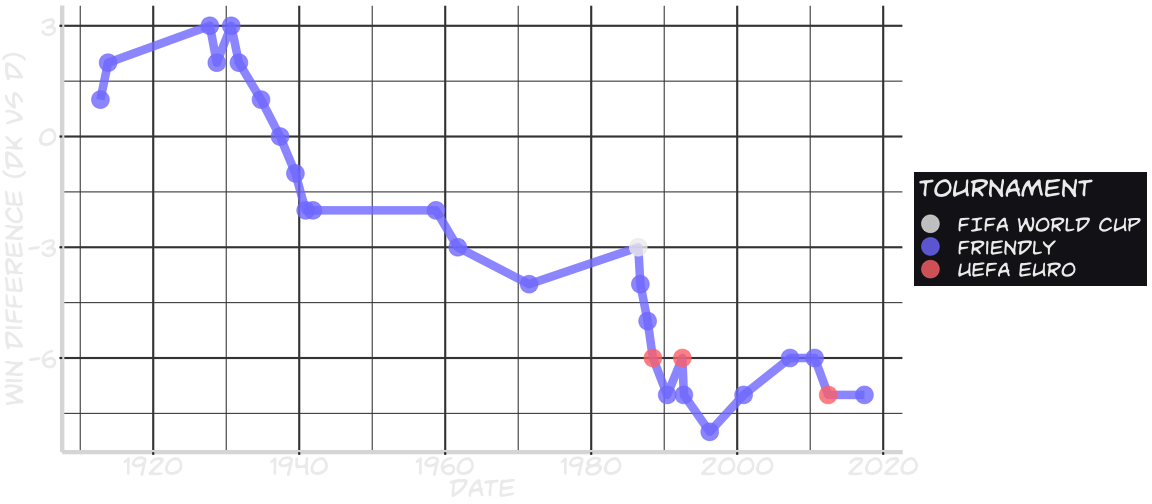

![](football_files/figure-html/unnamed-chunk-1-1.png)

---

???

Norsk Regnesentral. Norwegian computing center. Ville kopiere

Startede med EM 2012

---

# Predicting the world cup

"Simple" job

1.  Create function to model/predict a single match
2.  Run through tournament `$B$` times
3.  Get the predictions from the results

---

# Modeling a single match

ELO ratings. Two teams `$A$` and `$B$` with (external) ratings.

`$$P(\text{Team } A \text{ wins}) = \frac{1}{(1 + 10^{(\text{elo}_B - \text{elo}_A)/400})}$$`

```r
prob <- 1/(1 + 10^((elo[team2] - elo[team1])/400))
Awon <- rbinom(1, size=1, prob=prob)
```

After match: update ELO scores.

---

# Modeling a single match

Goals scored by each team simulated from two Poisson distributions.

*   Team A goals: `$\sim \text{Poiss}(\lambda_A)$`
*   Team B goals: `$\sim \text{Poiss}(\lambda_B)$`

Restrict `$\lambda_A$` and `$\lambda_B$` to use skill levels and make results realistic.

```r
Agoals <- rpois(1, lambdaA)
Bgoals <- rpois(1, normalgoals-lambdaA)
```

---

???

When is a prediction good?

---

# What makes a good prediction?

---

---

## Evaluating a prediction

.pull-left[
*   Take **all** predictions into account. Not just the winner.
*   Penalize **confident** classifications that are **incorrect**.
]

.pull-right[
Prediction: 32 x 32 matrix
.footnotesize[
```
      [,1] [,2] [,3] [,4] 
 [1,] 0.00 0.00 0.00 0.02 
 [2,] 0.00 0.00 0.00 0.04 
 [3,] 0.01 0.01 0.00 0.07 
 [4,] 0.00 0.00 0.01 0.08
```

Rows = ranks, 
columns = countries
]
]

>    *"It’s better to be somewhat wrong than emphatically wrong. 
>    Of course it’s always better to be right"*

---

# Log-loss

Heavily penalises confident classifications that are incorrect.

`$$-\sum_\text{ranking}\sum_\text{country}\unicode{x1D7D9}(\text{country c has rank r})\log(\hat{p_{rc}})$$`

**Problems**

*   It *feels* most important to correctly rank the top
*   No proper ordering for all but ranks 1-4
*   No representative data when match over. And then `$N=1$`.

---

# Weighted log-loss

To put more emphasis on the top positions add weights, `$w_r$`

`$$-\sum_\text{ranking}\sum_\text{country}w_r\cdot\unicode{x1D7D9}(\text{country c has rank r})\log(\hat{p_{rc}})$$`

**Weights:**

*   1 for ranks 1, 2
*   1/2 for ranks 3,4
*   1/4 for ranks 5-8
*   ...
---

# Missing ranks

We are missing ranks for all but the first 4.

**Solution**

Collapse probabilities into **7** rank groups: 1, 2, 3, 4, 5-8, 9-16, 17-32.

---

# Competition results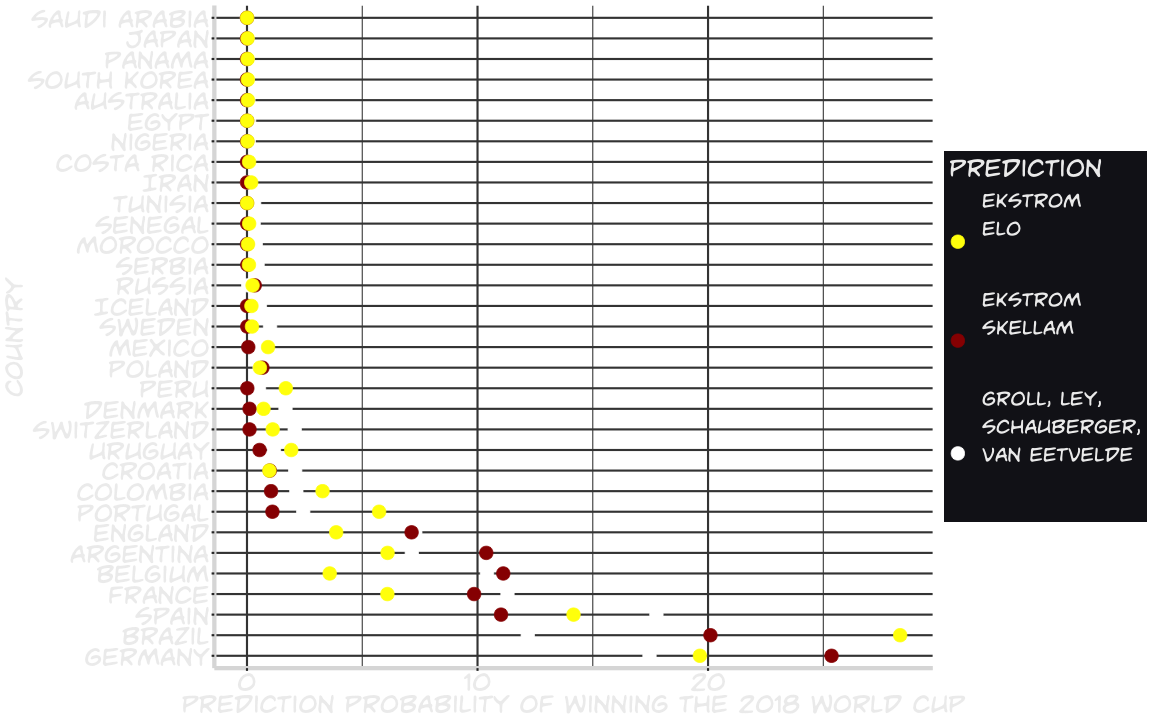

---

---

![](football_files/figure-html/unnamed-chunk-4-1.png)

---

# Results

|                                     | log.loss|
|:------------------------------------|--------:|
|Groll, Ley, Schauberger, VanEetvelde |   -11.69|
|Ekstrom (Skellam)                    |   -11.72|
|Ekstrom (ELO)                        |   -13.48|
|Random guessing                      |   -14.56|

---

# How can we improve the predictions?

---

# Ensemble predictions

>   *"This is how you win ML competitions: you take other peoples’ work and ensemble them together.” - Vitaly Kuznetsov*

---

# Bayseian model averaging

*   Use priors for each model, e.g., Schwarz' approximation

`$$P(M_j|Y) \approx \exp(-\frac12 \text{BIC}(M_j))$$`
    
    then
    
    `$$w(M_j) = \frac{\exp(-\frac12 \text{BIC}(M_j))}{\sum_{k=1}^K\exp(-\frac12 \text{BIC}(M_k))}$$`
    
???

Requires old data ....

Bayesian model

---

# Choice of loss function

What should the choice of loss function be?

*   Which extremes are we after?
*   Should be convex and proper scoring function

What should the weights be?

*   Which part of the ranks are important?
*   Should ensure proper scoring function

???

Convexity required for Jensen's inequality

---

# Improved modeling of single matches

*   Simple: Odds, ELO rankings, skills, ...

Typical models: bivariate, non-negative discrete Poisson / negative binomial. Look at **differences**

How to include predictors? How to fit their effects?

Instead ordinal outcome? L-T-W

Something else?

???

Correlation disappears.

May be needed for ties, but not strictly necessary

---

# Improved modeling of single matches

Drop parametric models and use other approaches:

*   Random forest
*   Neural networks (deep learning)

Primary interest: **prediction**. Less requirements on specific modeling.

How can we get data to train the models?

Model effect of players on teams?

---

# Resources

*   [International football results from 1872 to 2018](https://www.kaggle.com/martj42/international-football-results-from-1872-to-2017)
*   [European Soccer Database](https://www.kaggle.com/hugomathien/soccer)
*   [World Soccer - archive of soccer results and odds](https://www.kaggle.com/sashchernuh/european-football)

*   [Historic ELO ratings](https://www.eloratings.net/)

---

# Summary

Lots of interesting **statistical problems** to address.

Lots of interesting **decisions** to be made.

Create a computational framework for easy testing that makes

1.  comparisons easy
2.  possible to focus on the problems
3.  fast

Lots of possibilities for interesting **collaborations**